 |
pcb 4.1.1
An interactive printed circuit board layout editor.
|
 |
pcb 4.1.1
An interactive printed circuit board layout editor.
|
Go to the source code of this file.
Functions | |
| static gboolean | angle_obtuse (GtsVertex *v, GtsFace *f) |
| static gboolean | triangle_obtuse (GtsVertex *v, GtsFace *f) |
| static gdouble | cotan (GtsVertex *vo, GtsVertex *v1, GtsVertex *v2) |
| static gdouble | angle_from_cotan (GtsVertex *vo, GtsVertex *v1, GtsVertex *v2) |
| static gdouble | region_area (GtsVertex *v, GtsFace *f) |
| gboolean | gts_vertex_mean_curvature_normal (GtsVertex *v, GtsSurface *s, GtsVector Kh) |
| gboolean | gts_vertex_gaussian_curvature (GtsVertex *v, GtsSurface *s, gdouble *Kg) |
| void | gts_vertex_principal_curvatures (gdouble Kh, gdouble Kg, gdouble *K1, gdouble *K2) |
| static void | linsolve (gdouble m11, gdouble m12, gdouble b1, gdouble m21, gdouble m22, gdouble b2, gdouble *x1, gdouble *x2) |
| static void | eigenvector (gdouble a, gdouble b, gdouble c, GtsVector e) |
| void | gts_vertex_principal_directions (GtsVertex *v, GtsSurface *s, GtsVector Kh, gdouble Kg, GtsVector e1, GtsVector e2) |
Definition at line 64 of file curvature.c.
References GTS_POINT, gts_vector_init, gts_vector_scalar, and u().
Referenced by gts_vertex_gaussian_curvature().

Definition at line 23 of file curvature.c.
References GTS_POINT, GTS_SEGMENT, GTS_TRIANGLE, gts_triangle_edge_opposite(), gts_vector_init, and gts_vector_scalar.
Referenced by gts_vertex_principal_directions(), region_area(), and triangle_obtuse().

Definition at line 43 of file curvature.c.
References GTS_POINT, gts_vector_init, gts_vector_scalar, and u().
Referenced by gts_vertex_mean_curvature_normal(), gts_vertex_principal_directions(), and region_area().

| static void eigenvector | ( | gdouble | a, |
| gdouble | b, | ||
| gdouble | c, | ||
| GtsVector | e | ||
| ) | [static] |
Definition at line 305 of file curvature.c.
Referenced by gts_vertex_principal_directions().
| gboolean gts_vertex_gaussian_curvature | ( | GtsVertex * | v, |
| GtsSurface * | s, | ||
| gdouble * | Kg | ||
| ) |
gts_vertex_gaussian_curvature: : a GtsVertex. : a GtsSurface. : the Discrete Gaussian Curvature approximation at .
Computes the Discrete Gaussian Curvature approximation at .
This approximation is from the paper: Discrete Differential-Geometry Operators for Triangulated 2-Manifolds Mark Meyer, Mathieu Desbrun, Peter Schroder, Alan H. Barr VisMath '02, Berlin (Germany) http://www-grail.usc.edu/pubs.html
Returns: TRUE if the operator could be evaluated, FALSE if the evaluation failed for some reason ( is boundary or is the endpoint of a non-manifold edge.)
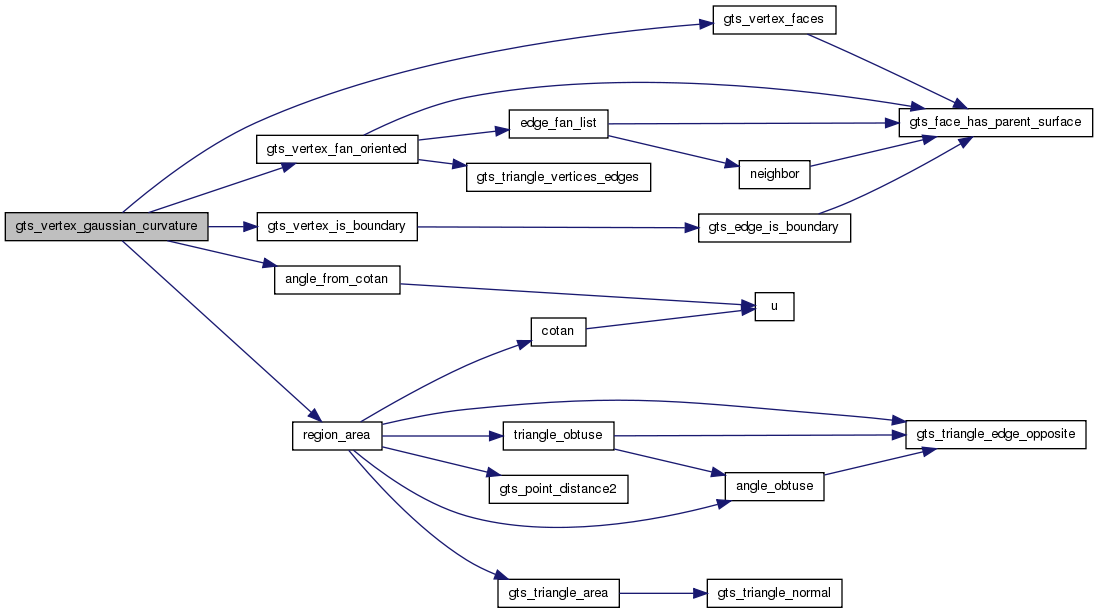
Definition at line 214 of file curvature.c.
References angle_from_cotan(), f, FALSE, GTS_SEGMENT, gts_vertex_faces(), gts_vertex_fan_oriented(), gts_vertex_is_boundary(), M_PI, region_area(), and TRUE.
| gboolean gts_vertex_mean_curvature_normal | ( | GtsVertex * | v, |
| GtsSurface * | s, | ||
| GtsVector | Kh | ||
| ) |
gts_vertex_mean_curvature_normal: : a GtsVertex. : a GtsSurface. : the Mean Curvature Normal at .
Computes the Discrete Mean Curvature Normal approximation at . The mean curvature at is half the magnitude of the vector .
Note: the normal computed is not unit length, and may point either into or out of the surface, depending on the curvature at . It is the responsibility of the caller of the function to use the mean curvature normal appropriately.
This approximation is from the paper: Discrete Differential-Geometry Operators for Triangulated 2-Manifolds Mark Meyer, Mathieu Desbrun, Peter Schroder, Alan H. Barr VisMath '02, Berlin (Germany) http://www-grail.usc.edu/pubs.html
Returns: TRUE if the operator could be evaluated, FALSE if the evaluation failed for some reason ( is boundary or is the endpoint of a non-manifold edge.)
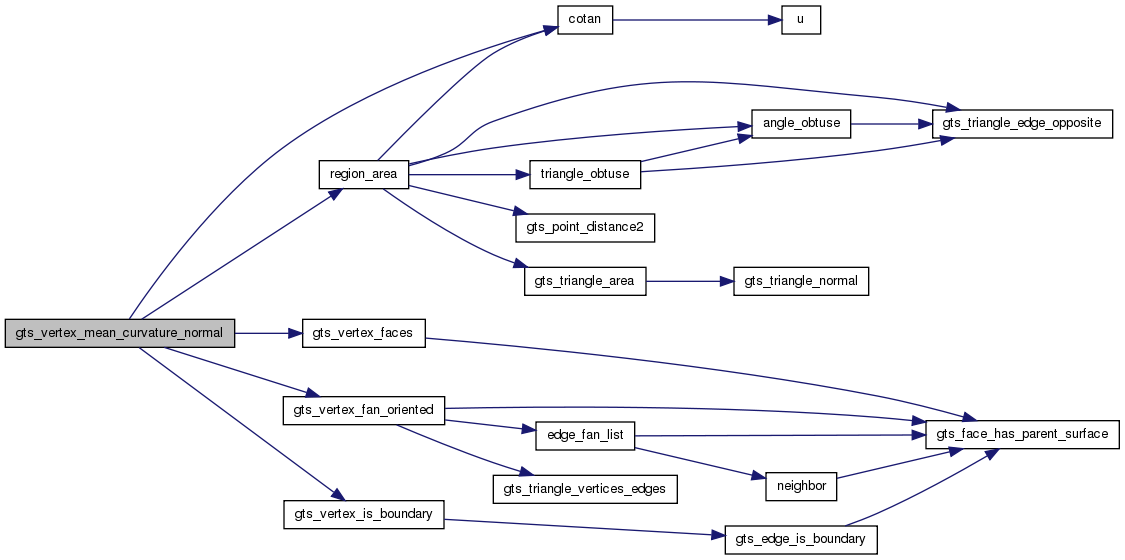
Definition at line 132 of file curvature.c.
References cotan(), f, FALSE, GTS_POINT, GTS_SEGMENT, gts_vertex_faces(), gts_vertex_fan_oriented(), gts_vertex_is_boundary(), region_area(), and TRUE.
| void gts_vertex_principal_curvatures | ( | gdouble | Kh, |
| gdouble | Kg, | ||
| gdouble * | K1, | ||
| gdouble * | K2 | ||
| ) |
gts_vertex_principal_curvatures: : mean curvature. : Gaussian curvature. : first principal curvature. : second principal curvature.
Computes the principal curvatures at a point given the mean and Gaussian curvatures at that point.
The mean curvature can be computed as one-half the magnitude of the vector computed by gts_vertex_mean_curvature_normal().
The Gaussian curvature can be computed with gts_vertex_gaussian_curvature().
Definition at line 278 of file curvature.c.
Referenced by gts_vertex_principal_directions().
| void gts_vertex_principal_directions | ( | GtsVertex * | v, |
| GtsSurface * | s, | ||
| GtsVector | Kh, | ||
| gdouble | Kg, | ||
| GtsVector | e1, | ||
| GtsVector | e2 | ||
| ) |
gts_vertex_principal_directions: : a GtsVertex. : a GtsSurface. : mean curvature normal (a GtsVector). : Gaussian curvature (a gdouble). : first principal curvature direction (direction of largest curvature). : second principal curvature direction.
Computes the principal curvature directions at a point given and , the mean curvature normal and Gaussian curvatures at that point, computed with gts_vertex_mean_curvature_normal() and gts_vertex_gaussian_curvature(), respectively.
Note that this computation is very approximate and tends to be unstable. Smoothing of the surface or the principal directions may be necessary to achieve reasonable results.
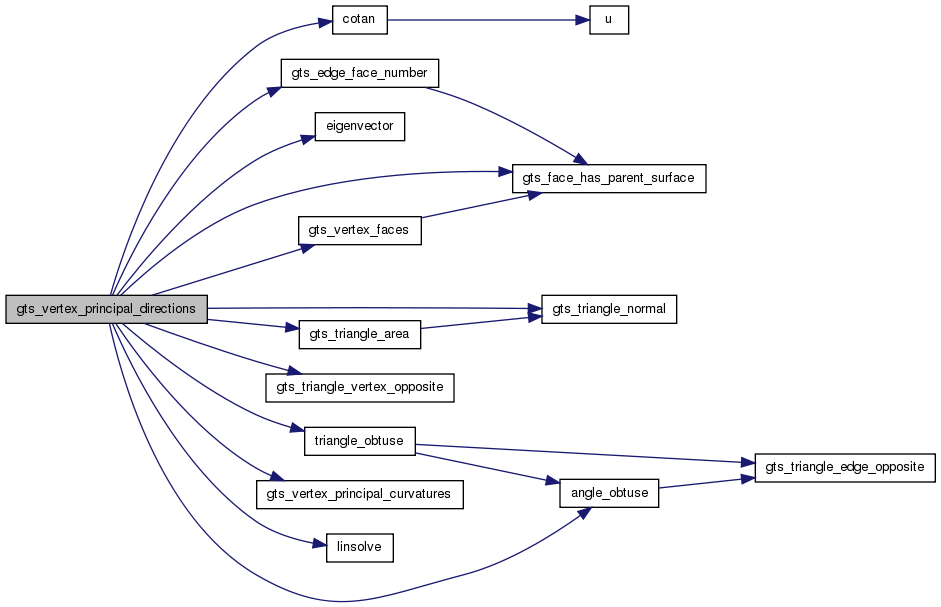
Definition at line 335 of file curvature.c.
References angle_obtuse(), c, cotan(), eigenvector(), gts_edge_face_number(), GTS_FACE, gts_face_has_parent_surface(), GTS_IS_EDGE, GTS_IS_FACE, GTS_POINT, GTS_SEGMENT, GTS_TRIANGLE, gts_triangle_area(), gts_triangle_normal(), gts_triangle_vertex_opposite(), gts_vector_cross, gts_vector_init, gts_vector_norm, gts_vector_normalize, gts_vector_scalar, gts_vertex_faces(), gts_vertex_principal_curvatures(), linsolve(), N, _GtsVertex::segments, triangle_obtuse(), _GtsEdge::triangles, x, and y.
| static void linsolve | ( | gdouble | m11, |
| gdouble | m12, | ||
| gdouble | b1, | ||
| gdouble | m21, | ||
| gdouble | m22, | ||
| gdouble | b2, | ||
| gdouble * | x1, | ||
| gdouble * | x2 | ||
| ) | [static] |
Definition at line 293 of file curvature.c.
Referenced by gts_vertex_principal_directions().
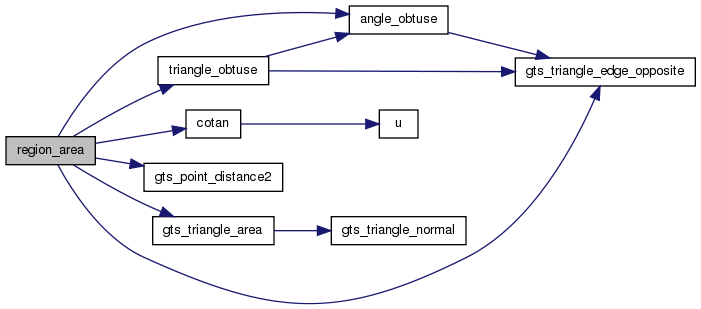
Definition at line 84 of file curvature.c.
References angle_obtuse(), cotan(), GTS_POINT, gts_point_distance2(), GTS_SEGMENT, GTS_TRIANGLE, gts_triangle_area(), gts_triangle_edge_opposite(), and triangle_obtuse().
Referenced by gts_vertex_gaussian_curvature(), and gts_vertex_mean_curvature_normal().
Definition at line 34 of file curvature.c.
References angle_obtuse(), GTS_SEGMENT, GTS_TRIANGLE, and gts_triangle_edge_opposite().
Referenced by gts_vertex_principal_directions(), and region_area().
